USAMTS Problem 1/2/15

 

The faces of 27 unit cubes are painted red, white, and blue in such a manner that we can assemble them into three different configurations: a red 3 x 3 x 3 cube, a white 3 x 3 x 3 cube, and a blue 3 x 3 x 3 cube.  Determine, with proof, the number of unit cubes on whose faces all three colors appear.

 

Let a “unit-face” be defined as the face of a unit cube.

 

Each unit cube has six unit-faces, so with 27 unit cubes we have a total of 162 unit-faces.

 

Each 3 x 3 x 3 cube has 6(9) = 54 unit-faces showing.

 

Since the unit cubes can be arranged in the 3 x 3 x 3 cube with red, white, and blue faces showing, respectively, there must be at least 54 unit-faces of each color.  However, since the total number of unit-faces is 162 (= 54 + 54 + 54), we must have exactly 54 unit-faces of each color.

 

Taking the red 3 x 3 x 3 cube, all of the red unit-faces must be showing, and none of the “inner faces” (the faces not showing) may be red.

 

Also, there are exactly 8 “corner” unit cubes with 3 red faces, 12 “edge” unit cubes with 2 red faces, 6 “central” unit cubes with one red face, and 1 “inner” unit cube with no red faces.

 

Thus, exactly one unit cube contains no red faces; it must have 3 white faces and 3 blue faces.

 

Similarly, taking the white and blue 3 x 3 x 3 cubes, exactly one unit cube contains no white faces, and exactly one unit cube contains no blue faces.

 

Thus, we have exactly three unit cubes that contain only two different colors among their faces; the rest have all 3 different colors among their faces.

 

24 cubes must contain all three colors among their faces.

 

We can easily show that one can have this arrangement having:

 

3 cubes with                 (3-3-0,  3-0-3,  0-3-3)

18 cubes with               (3 each of the type 3-2-1,  3-1-2,  2-3-1,  2-1-3,  1-3-2,  and 1-2-3)

6 cubes with                 (6 of the type 2-2-2)

 

(Note: “3-2-1” means a unit cube having 3 red faces, 2 white faces, and 1 blue face, etc…)

 

Thus, for a 3 x 3 x 3 red cube, we will have 8 corner pieces (3-3-0,  3-0-3,  3 (3-2-1)’s and
3 (3-1-2)’s), 12 edge pieces (6 (2-2-2)’s,  3 (2-1-3)’s, and 3 (2-3-1)’s), and 6 central pieces with 1-x-x.  The inner cube is 0-3-3.  Similar arrangements can be made for the other
3 x 3 x 3 configurations.

USAMTS Problem 2/2/15

 

For any positive integer n, let s(n) denote the sum of the digits of n in base 10.  Find, with proof, the largest n for which n = 7s(n).

 

Let a, b, c, d, … be the digits of n when n is written in base 10.  (a is the unit digit, b the ten, c, the hundred, etc.)

Then,

n = a + 10b + 100c + 1000d + …

and

s(n) = a + b + c + d + …

 

If n = 7s(n), then

a + 10b + 100c + 1000d + … = 7a + 7b + 7c + 7d + …

or

6a = 3b + 93c + 993d + …

 

Since a < 9, the left side of this is 6a < 54.

This implies that c = d = e = … = 0.

 

So, 6a = 3b, or

2a = b

 

Since b < 9,

a < (9 / 2) < 4.

 

The maximum value of n occurs when a = 4 and b = 8.

 

So, the largest value for n = 7s(n) is n = 84.

USAMTS Problem 3/2/15

 

How many circles in the plane contain at least three of the nine points (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)?  Rigorously verify that no circle was skipped or counted more than once in the result.

 

For easier reference, let us label the nine points as follows:

We have 9 points, and so we have  = 84 sets of 3 points.

A circle can be circumscribed about any triangular set of 3 points.

 

A circle cannot be circumscribed about 3 collinear points, so we ignore the sets

{ABC}, {DEF}, {GHI}, {ADG}, {BEH}, {CFI}, {AEI}, and {CEG}

 

We have 84  8 = 76 triangular sets of points.

 

Some of these triangles will be circumscribed by a common circle. 

 

Any set of four points that forms a rectangle (rectangles include squares) will be circumscribed by a single circle.  There are a total of 10 such rectangular sets:

{ABED}, {BCFE}, {EFIH}. {DEHG}, {ACFD}, {DFIG}, {ABHG}, {BCIH}, {DBFH}, and {ACIG}

 

Also, each of the 4-point sets {ABFI}, {CFHG}, {IHDA}, and {GDBC} is circumscribed by a single circle.  (The opposite angles of this figure  45° and 135°  sum to 180°.)

 

We can prove that there are no circles which pass through 5 (or more) points.

Let us divide the nine points into 3 groups:

Group A, the 4 corner points {A, C, G, I},
Group B, the 4 “edge” points {B, D, F, H},
and Group C, the central point {E}.

Since Group A is a square, a circle passing through any 3 of its points is a unique circle (which circumscribes the square).  Similarly, a single circle circumscribes the points in group B.  So, we cannot select 3 (or more) points from any group, and thus it is not possible for any circle to go through 6 or more points, and the only possibility for a 5 point circle is a 2-2-1 arrangement or a circle passing through the center point (E) and two corners.  These arrangements are contradictions because they will either form straight lines (diagonal AEI or CEG) or a three point circle (e.g. ACE).

 

For each circumscribable set of four points, we are counting the same circle four times; to obtain the number of unique triangles formed, we ignore 3 of the triangles formed for each of these four point sets.

 

This leaves us with a total of 76  3(10 + 4) = 34 circles.

 

(I have also systematically counted all the three point combinations and confirmed that the answer is indeed 34.)

 

1	ABC	St. Line	29	BCD	BCDG circle	57	CEH
2	ABD	ABDE circle	30	BCE	BCEF circle	58	CEI
3	ABE	Same as #2	31	BCF	Same as #30	59	CFG	CFGH circle
4	ABF	ABFI circle	32	BCG	Same as #29	60	CFH	Same as #59
5	ABG	ABGH circle	33	BCH	BCHI circle	61	CFI	St. Line
6	ABH	Same as #5	34	BCI	Same as #33	62	CGH	Same as #59
7	ABI	Same as #4	35	BDE	Same as #2	63	CGI	Same as #11
8	ACD	ACDF circle	36	BDF	BDFH circle	64	CHI	Same as #33
9	ACE		37	BDG	Same as #29	65	DEF	St. Line
10	ACF	Same as #8	38	BDH	Same as #36	66	DEG	DEGH circle
11	ACG	ACGI circle	39	BDI		67	DEH	Same as #66
12	ACH		40	BEF	Same as #30	68	DEI
13	ACI	Same as #11	41	BEG		69	DFG	DFGI circle
14	ADE	Same as #2	42	BEH	St. Line	70	DFH	Same as #36
15	ADF	Same as #8	43	BEI		71	DFI	Same as #69
16	ADG	St. Line	44	BFG		72	DGH	Same as #66
17	ADH	ADHI circle	45	BFH	Same as #36	73	DGI	Same as #69
18	ADI	Same as #17	46	BFI	Same as #4	74	DHI	Same as #17
19	AEF		47	BGH	Same as #5	75	EFG
20	AEG		48	BGI		76	EFH	EFHI circle
21	AEH		49	BHI	Same as #33	77	EFI	Same as #76
22	AEI	St. Line	50	CDE		78	EGH	Same as #66
23	AFG		51	CDF	Same as #8	79	EGI
24	AFH		52	CDG	Same as #29	80	EHI	Same as #76
25	AFI	Same as #4	53	CDH		81	FGH	Same as #59
26	AGH	Same as #5	54	CDI		82	FGI	Same as #69
27	AGI	Same as #11	55	CEF	Same as #30	83	FHI	Same as #76
28	AHI	Same as #17	56	CEG	St. Line	84	GHI	St. Line

 

 

The systematic count of unique circles (in bold above) is 34.

USAMTS Problem 4/2/15

 

In how many ways can one choose three angle sizes, α, β, and γ, with α < β < γ from the set of integral degrees, 1°, 2°, 3°, …, 178°, such that those angle sizes correspond to the angles of a nondegenerate triangle?  How many of the resulting triangles are acute, right, and obtuse, respectively?

 

γ is the largest (or equal to another of the largest) angle of a triangle; when 91° < γ < 178°, we have an obtuse triangle; when γ = 90°, we have a right triangle, and when 60° < γ < 89°, we have an acute triangle.  Obviously, γ cannot be less than 60°.

 

For obtuse triangles:

(Even, γ = 2n;                        92° < 2n < 178°, or 46° < n < 89°)

For each γ we have  unique sets {α, β}. 

Since γ = 2n, for each even γ we have 90  n obtuse triangles.

 

(Odd, γ = 2n  1;     91° < (2n  1) < 177°, or 46° < n < 89°)

For each γ we have  unique pairs {α, β}. 

Since γ = 2n  1, for each odd γ we also have 90  n obtuse triangles.

 

Total number of obtuse triangles:

 = 1980 unique obtuse triangles.

 

For right triangles:

When γ = 90°, we have  = 45 pairs {α, β}.  So, we have 45 unique right triangles.

 

For acute triangles:

(Even, γ = 2n;                        60° < 2n < 88°, or 30° < n < 44°)

For each even γ, we have  or 3n  89 acute triangles.

(Odd, γ = 2n + 1;      61° < (2n + 1) < 89°, or 30° < n < 44°)

 

For each odd γ, we have  or 3n  88 acute triangles.

 

Total number of acute triangles:

 
                                                                                                = 675 unique acute triangles.

 

 

USAMTS Problem 5/2/15

 

Clearly draw or describe a convex polyhedron that has exactly three pentagons among its faces and the fewest edges possible.  Prove that the number of edges is a minimum.

 

A pentagon has five corners.  If we ignore duplicate corners, three pentagons will have 15 corners. 

 

Each pair of pentagons on a polyhedron can have at most two common corners.  (Three common corners would make them lie on the same plane.)  With three pentagons, at most 6 corners may be shared.

 

So, a polyhedron with three pentagons among its faces must have at least 15  6 = 9 corners.

 

A minimum of three edges meet at each corner of a polyhedron.  Thus, since there are a minimum of 9 corners, we must have at least 9 * 3 = 27 “meeting edges.”  This is double-counting all of the edges since each edge has two corners, and is counted twice.

 

So, the number of edges must be greater than (27 / 2), and since it must be an integer, it must be greater than or equal to 14.

 

Below is an example of a 14-edged polyhedron with three pentagonal faces:

 

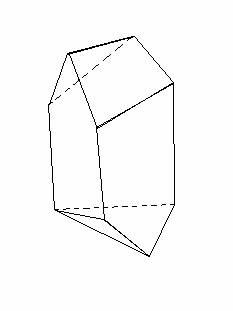
(I have constructed this figure with cardboard to confirm its validity.)

 

The figure above contains 9 corners, 14 edges, and 7 faces (3 pentagons, 3 triangles, and 1 quadrilateral). 

 

There may be other solutions, but no other polyhedron will have a lesser number of edges.