USAMTS Problem 1/3/12
Find the smallest positive integer with the property that it has divisors ending with every decimal digit, i.e., divisors ending in 0, 1, 2, …, 9.
Let such a number be N. We will determine the prime factors of N
Since any number ending in a 0 is a multiple of 10, and N is a multiple of this number, N must be a multiple of 10.
Thus 5 and 2 must be factors of N.
We now do not have to worry about 1, 2, and 5 (and 0) if the above condition is met.
Now let us check for the numbers which are prime to 10. These numbers are 3, 7, and 9.
(N/10) must have a divisor, of the form “a” ending in 3 (a ≡ 3 (mod 10)).
It must have another divisor, of the form “b” ending in 7 (b ≡ 7 (mod 10)) (Because a multiplied by 2 or 5 can not end in 7)
It must still have another divisor, of the form “c” ending in 9 (Again neither a nor b can end in 7 when multiplied by 2 or 5)
We will consider cases when (N/10) has 1, 2, ... distinct prime factors other than 2 and 5.
If (N/10) has only one distinct prime factor other than 2 and 5, it must be of the form p^3, to give 3 divisors of the form a, b, c (p, p2, p3).
If (N/10) has two distinct prime factors other than 2 and 5, they can be of the form q and r
(so that q, r and q · r are of the form a, b and c)
The smallest possible value of p is 3. It does work. (32 ≡ 9 (mod 10), and 33 ≡ 7(mod 10)) to produce the divisors of the form a, b and c)
It is also easy to check that 2 · 3 ≡ 6 (mod 10), 2 · 32 ≡ 8(mod 10), 2 · 33 ≡ 4 (mod 10)
For the case where (N/10) has 2 distinct prime factors (other than 2 and 5), the smallest case which works is 3 · 19 which is larger than 33. For more than 3 distinct primes (N/10) will be larger than 33. Thus the above case is the smallest possible number.
N = 2 · 5 · 33 = 270
(One can check that it is divisible by 1, 2, 3, 54, 5, 6,
27, 18, 9 and 10)
USAMTS Problem
Assume that the irreducible fractions between 0 and 1,
with denominators at most 99, are listed in ascending order. Determine which two fractions are adjacent to
in this listing.
Let us call the two adjacent fractions .
We define “adjacent” and by adjacent we mean that there are no
fractions of the type (x and y are integers, and
) in the range
and
.
Since ,
we can say both a and c are less than 24.
If we take the reciprocal of all the fractions in the given set, then the same corresponding fractions will be adjacent, but in the opposite order. This gives us
a and c both less than 24.
(These are “adjacent” if and only if the original fractions are adjacent)
Now,
,
(
)
,
(
)
So,
,
and these fractions are “adjacent”, with c and a are less than
24.
We can use the same method again for our new set of fractions:
.
We can take the reciprocal of all our fractions again, getting
,
b1 and d1 are both less than 13, and the
fractions are adjacent.
Now we have:
.
,
(
)
,
(
)
So,
,
b1 and d1 are both less than 13, and the
fractions are adjacent.
Thus it is easy to see,
,
and
.
,
,
Thus,
,
and
:
, are
“adjacent” (for denominators less than or equal to 99).
USAMTS Problem 3/3/12
Let have roots
. Let
. Determine the product
.
First, we note that an equation of the form
with roots can be written:
,
or
So,
From this we can say that, in our given equation with roots
,
We are trying to find ,
that is,
.
We can find (a is a number), because it is just
,
or
We can also find the same way:
,
or
If we multiplied these last two results, (remember that )
we would get
If we let ,
we get:
= -23
USAMTS Problem 4/3/12
Assume that each member of the sequence is either a + sign or a
sign.
Determine the appropriate sequence of + and
signs so that
Also determine what sequence of signs is necessary if the sixes in the nested roots are replaced by sevens. List all integers that work in the place of sixes and the sequences of signs that are needed with them.
First, we can square both sides:
1
must be a
sign because
denotes the positive square root of x.
…
We are back where we started, so the cycle will repeat and
the i’s
are all
signs.
In the case of seven, we have
1
must be a
sign.
2
must be a + sign.
…
Thus the cycle repeats, and our sequence is ,
+,
,
+, …
The number 4 will be subtracted from our number x in
the nested roots during the first step.
This result will then be squared.
If ,
then when we subtract x again, we will get a number greater than 2, and
as we square and subtract again and again, our number will get larger and
larger, and will never come back to 2.
Thus we can write the inequality to find out what our possibilities for x are:
Now, we just need to test 2, 3, 4, and 5. (We already know the correct sequences for 6 and 7.)
Test for 2:
1
must be a + sign.
…
The cycle repeats, the sequence is all +’s.
Test for 3:
1
must be a + sign.
2
must be a
sign.
…
Thus the cycle continues, and the sequence is +. ,
+,
,
…
Test for 4:
…
The cycle will repeat, and the left side will keep increasing, and never become 2.
4 does not work.
Test for 5:
…
The cycle will repeat, and the left side will keep increasing, and never become 2.
5 does not work.
So, the only values that work for x in the equation
are 2, 3, 6, and 7.
The sequence of + and signs for each of them is:
2: all + signs
3: +, .
+,
,
…
6: all signs
7: ,
+,
,
+, …
 USAMTS Problem
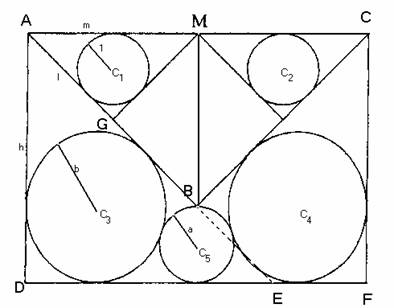
USAMTS Problem 5/3/12
Three isosceles right triangles are
erected from the larger side of a rectangle
into the interior of the rectangle, as show
on the right, where M is the midpoint of
that side. Give circles are inscribed
tangent to some of the sides and to one
another as shown. One of the circles
touches the vertex of the largest triangle.
Find the rations among the radii of the
five circles.
(1) First, we show the ratio of the length of a leg s of an isosceles right triangle to the
length of a radius of an inscribed circle. The length of an altitude drawn to the
hypotenuse of our triangle is equal to the length of the radius r plus
the length of a diagonal of a square with a side length of r: . (See Fig. 1)
Thus we get the equation:
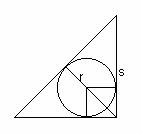
Figure 1
.
(2) We also will find the distance between the points
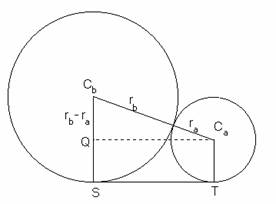 of
tangency S and T of two tangent circles
of
tangency S and T of two tangent circles and
on a common external tangent
in terms
of their radii and
. (See Fig. 2)
If we draw
a segment perpendicular to
,
it will
have the same length as because
and are parallel.
This forms a right triangle,
Figure 2
with hypotenuse of length
and a leg of
length . Now we can use the Pythagorean Theorem to
find our missing side :
Therefore,
.